An introduction to Mascot Daemon
Mascot Daemon is a Microsoft Windows client application that automates the submission of data files to Mascot server. Functionality includes:
- Batch mode, in which an arbitrary group of files can be defined for searching, either immediately or at some pre-set time.
- Real-time monitor mode, in which new files on a pre-defined path are searched as they are created.
- Data dependent follow-up tasks. For example, automatically repeating a search at a later date or against a different sequence database.
Multiple Daemon clients can submit searches to the same Mascot server. If you have several mass spectrometers, you can install separate copies of Daemon on each instrument data system or just have a single copy of Daemon somewhere on the LAN processing searches for data from all instruments.
The functional unit of Mascot Daemon is a task, which is defined by the data source (a list of data files or a file path), how the data are to be searched, when the searches are to take place, and any follow-up activities, such as conditional repeat searches.
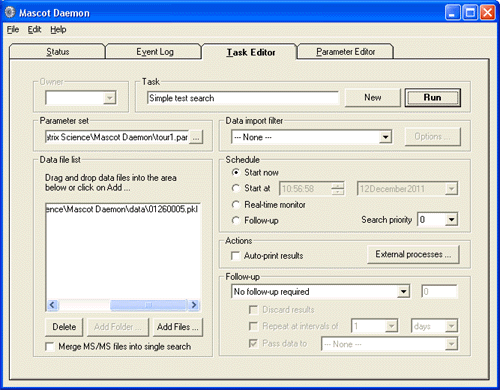
Setting up a task
Search parameters are defined in the Parameter Editor, which closely resembles the HTML form used for interactive Mascot searches. Fields can also contain HTML-like tags which are automatically substituted at run time with information such as a file name or a sample description.
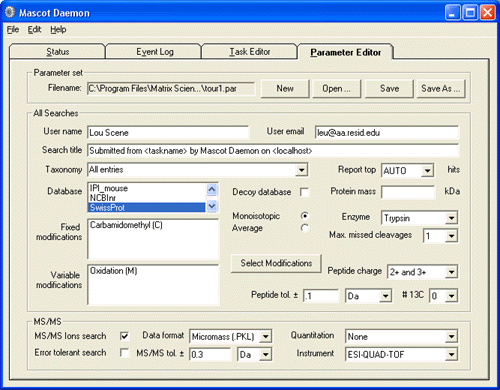
Search Parameter editor
Every time a new task is run, it creates a task node on the status tree. The results from each task are attached to the task node, just like directories and sub-directories in Windows Explorer. Key information for each result can be displayed by clicking on the result node. The full result report can be displayed in a web browser by clicking on the blue hyperlink.
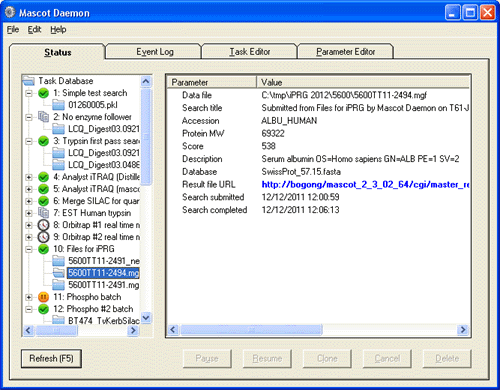
A result on the status tree
Daemon’s follow-up function can be used in many different ways. A couple of simple examples would be:
- A batch of data files can be searched at specified intervals against database updates. Each data file will stay in the loop until it’s score exceeds a pre-set level.
- Sequence databases of increasing size or decreasing quality can be searched serially. For example, a small database of common contaminants might be searched first. Spectra which are unmatched can then be searched against a comprehensive non-redundant protein database, such as NCBIprot. Data which still fail to find a match can then proceed to a search of an EST database.
Arbitrary numbers of follow-up tasks can be chained together to implement complex decision trees. This is possible because Mascot scores reflect true probabilities, permitting rule based software to determine whether a match is significant according to user specified criteria.
The default database engine used by Mascot Daemon is Microsoft Jet 4.0, the engine used by Microsoft Access. Alternatively, Daemon can be configured to use any database engine which supports either OLE DB or ODBC, such as Microsoft SQL-Server or Oracle, enabling multiple Daemon clients to share a common task database.

